La physique quantique n’est pas simplement une avancée technique ou une curiosité scientifique, elle constitue une refondation complète de notre manière de concevoir la réalité. Dans le monde macroscopique, les objets ont une position définie, des trajectoires continues, des causes et des effets clairs. Mais dès que l’on entre dans le monde des particules, des atomes et des photons, ce cadre explose. Le quantique introduit des notions contre-intuitives, mais puissantes : la superposition, l’incertitude, l’intrication, et un formalisme mathématique totalement nouveau.
Une révolution conceptuelle
Au début du XXe siècle, la physique classique semblait presque achevée. Pourtant, plusieurs phénomènes refusaient obstinément d’y entrer. Le rayonnement du corps noir, l’effet photoélectrique, et les raies spectrales des atomes ne pouvaient être expliqués sans faire une hypothèse audacieuse : l’énergie est émise par paquets discrets, que l’on appellera bientôt quanta.
Cette idée fondatrice naît en 1900, avec Max Planck. Il découvre que l’énergie d’un oscillateur ne peut varier que par multiples de la constante multipliée par une fréquence :
E = nhv
Cette simple équation annonce le passage à une nouvelle physique, la physique quantique.
Les piliers de la mécanique quantique
La superposition
L’une des idées les plus dérangeantes — et les plus fécondes — est celle de superposition. Dans le monde quantique, un système ne se trouve pas nécessairement dans un état bien défini, mais dans plusieurs états à la fois. C’est comme si une pièce en rotation pouvait être à la fois face et pile tant qu’on ne l’a pas regardée.
Prenons l’exemple du qubit, l’équivalent quantique du bit informatique. Un bit classique est soit 0, soit 1. Mais un qubit peut être dans une superposition des deux, mathématiquement cela nous donne :
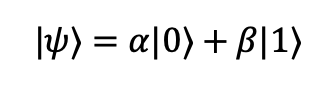
La superposition n’est pas un artefact : c’est ce qui permet aux ordinateurs quantiques de manipuler en parallèle une multitude d’états et donc de diminuer drastiquement la vitesse de calcul.
L’intrication : deux particules, une seule réalité
Une autre caractéristique stupéfiante du quantique est l’intrication. Lorsque deux particules interagissent dans certaines conditions, elles peuvent devenir intriquées : leur état global ne se décompose plus en deux états indépendants. En d’autres termes, ce qui arrive à l’une affecte instantanément l’autre, quelle que soit la distance. Un état intriqué entre deux qubits serait :
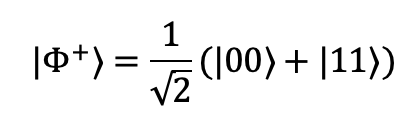
Dans cet état, ni la première ni la deuxième particule n’a une valeur propre. Mais la mesure de l’une détermine immédiatement l’état de l’autre. Si l’on mesure le premier qubit et qu’il donne 0, le second sera 0 ; s’il donne 1, l’autre aussi. C’est une propriété non locale du réel, vérifiée expérimentalement. L’expérience de Bella a montré que ces corrélations ne peuvent pas s’expliquer par une théorie classique sous-jacente. L’intrication est aujourd’hui une ressource : elle permet la téléportation d’états quantiques ou la cryptographie parfaitement sécurisée.
L’incertitude : une limite fondamentale de la connaissance
Dans la physique classique, connaître la position et la vitesse d’un objet permet de prédire son comportement futur. Mais en mécanique quantique, cette double connaissance est fondamentalement impossible. Le principe d’incertitude de Heisenberg énonce que :
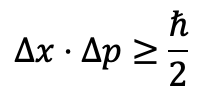
Nous notons delta x l’incertitude sur la position tandis que delta p est l’incertitude sur la qualité du mouvement. Plus on localise une particule, plus son impulsion devient indéterminée, et inversement. Ce n’est pas un défaut de mesure, mais une propriété profonde du monde. Il n’existe pas de trajectoire définie à tout instant, seulement des probabilités de présence. On retrouve notamment cette propriété dans le modèle de Bohr[1] – quantique -.
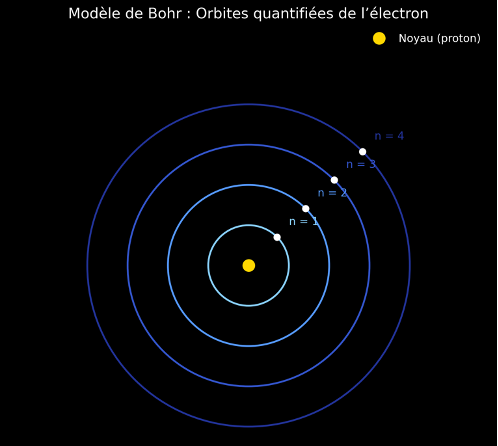
La matière confinée dans les puits quantiques
Imaginons une particule enfermée entre deux barrières infranchissables. En mécanique classique, elle pourrait avoir n’importe quelle énergie et se déplacer librement à l’intérieur. Mais en mécanique quantique, seules certaines formes d’ondes stationnaires sont autorisées. La particule n’a plus une position définie mais une fonction d’onde qui décrit sa probabilité de présence. Cette onde doit s’annuler aux bords du puits, ce qui impose des conditions mathématiques strictes :
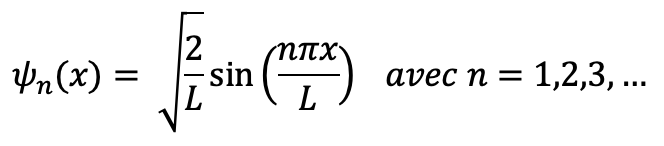
Les énergie associées doivent aussi être discrètes :
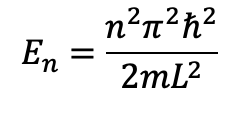
Autrement dit, une particule confinée ne peut pas avoir n’importe quelle énergie, mais seulement certaines valeurs quantifiées, comme les notes d’un instrument de musique. Plus le niveau est élevé, plus l’onde est complexe, plus l’énergie est grande.
Ces puits quantiques sont aujourd’hui au cœur de technologies de pointe, des puces optoélectroniques aux nanostructures quantiques, en passant par les boîtes quantiques utilisées en informatique quantique ou en photonique.
Une équation pour tout gouverner
L’un des plus grands apports de la physique quantique est d’avoir identifié une nouvelle manière de penser l’évolution des systèmes physiques. À la place des trajectoires continues de la mécanique classique, elle propose une description fondée sur une entité étrange et puissante : la fonction d’onde.
Cette fonction, notée psi, contient toute l’information disponible sur un système quantique. Elle permet de connaître, non pas où se trouve précisément une particule, mais avec quelle probabilité elle peut être détectée ici ou là, avec telle ou telle valeur d’impulsion, ou d’énergie. C’est elle qui fait le lien entre les mathématiques et la mesure physique.
L’équation de Schrödinger décrit comment cette fonction évolue dans le temps. Il s’agit de l’équation fondamentale du quantique, tout comme la deuxième loi de Newton est celle du monde classique. Elle s’écrit :
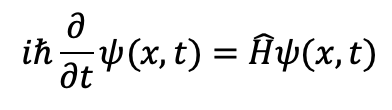
Nous y retrouvons ici psi(x,t), la fonction d’onde dépendante du temps et de la position, h la constante de Planck et H, l’Hamiltonien, celui-ci correspond à l’énergie totale du système, il combine l’énergie cinétique et le potentiel, selon les caractéristiques du système étudié. Ce qui rend l’équation de Schrödinger si fascinante, c’est qu’elle n’est pas elle-même probabiliste. Donnez-lui une fonction d’onde initiale psi(x,0) et elle vous fournira une fonction psi(x,t) pour tout t, sans ambiguïté. En ce sens, elle est parfaitement déterministe.
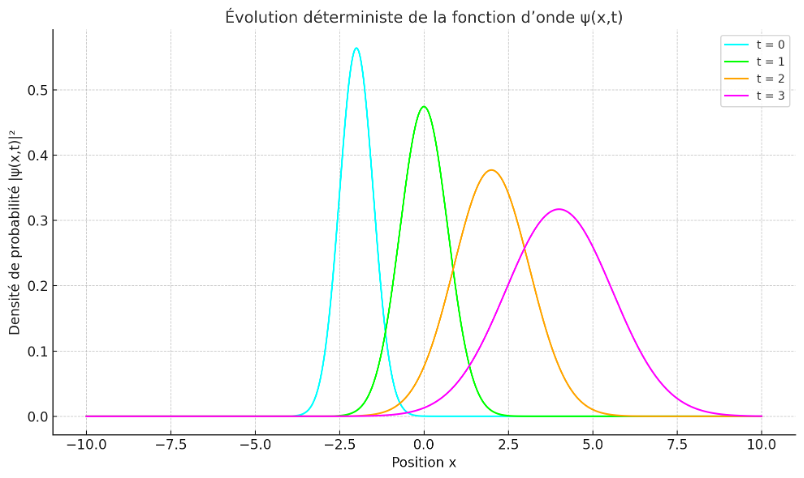
Il est cependant à noter que l’objet qu’elle fait évoluer – psi – n’est pas une grandeur mesurable. Ce que nous mesurons, ce sont des positions, des énergies, des impulsions — et ces mesures sont gouvernées par la probabilité :
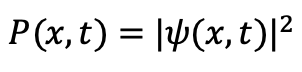
Ainsi, ce que décrit Schrödinger, ce n’est pas le comportement d’une particule, mais celui d’une distribution de présence, une structure d’amplitudes complexes dont le carré donne une densité de probabilité.
L’équation de Schrödinger ne dépend pas du type de système : elle s’applique à tous les objets quantiques. Ce qui change, c’est l’Hamiltonien, pour un électron libre, il ne contient qu’une partie cinétique. Pour une particule dans un champ électrique ou magnétique, il inclut les effets du potentiel. Pour un atome, il intègre les interactions internes. Mais la forme de l’équation reste identique.
Ce caractère universel fait de Schrödinger le langage fondamental de la dynamique quantique. Que l’on parle d’un électron dans un microscope, d’un neutron dans un cristal, ou d’un photon dans une cavité optique, c’est toujours cette équation qui détermine l’évolution de l’état.
[1] https://facmed.univ-constantine3.dz/wp-content/uploads/2021/11/th%C3%A9orie-de-BOHR.pdf










